728x90
반응형

코헨의 카파(Cohen's kappa, κ) 점수는 두 관찰자가 어떤 항목을 분류할 때 얼마나 일치하는지, 그리고 그 일치도가 우연 때문이 아닌지를 평가하는 지표이다.
예를 들어, 두 사람이나 딥러닝 모델이 소셜 미디어 게시물을 검토하고 '적절함' 또는 '부적절함'으로 분류한다고 가정해 봤을 때, 두 평가자(또는 모델)가 얼마나 일치했는지를 확인하려면 코헨의 카파 점수를 계산할 수 있다.
공식:
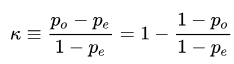
- p_o: 관찰된 일치 비율, 즉 평가자들이 실제로 일치한 비율을 의미
- p_e: 우연히 일치할 가능성을 나타내는 기대 일치 비율
값의 해석:
- κ=1: 완전한 일치.
- κ=0: 우연과 동일한 수준의 일치.
- κ<: 우연보다 낮은 수준의 일치.
보통 다음과 같이 해석한다:
- 0.81–1.00: 거의 완벽한 일치.
- 0.61–0.80: 상당한 일치.
- 0.41–0.60: 중간 수준의 일치.
- 0.21–0.40: 보통 수준의 일치.
- 0.00–0.20: 약간의 일치.
- < 0.00: 일치하지 않음.
예시: 소셜 미디어 부적절한 게시물 검토
A와 B는 소셜 미디어 게시물을 검토하고, 각각 "적절함" (1) 또는 "부적절함" (0)으로 분류합니다. 두 사람이 얼마나 일치했는지 확인하려면 코헨의 카파 점수를 계산할 수 있습니다.
데이터 예시
게시물: 1 2 3 4 5 6 7 8 9 10
관리자 A: 1 0 1 1 0 0 1 0 1 1
관리자 B: 1 0 1 0 0 0 1 1 1 1
코헨의 카파 계산:
- p_o: 관찰된 일치 비율. 두 사람이 일치한 경우는 게시물은 총 8개이다.
p_o = 8/10 = 0.8 - p_e:
적절함이라고 말할 확률: A(6/10) x B(6/10) = 0.36
부적절함이라고 말할 확률: A(4/10) x B(4/10) = 0.16
p_e = 0.36 + 0.16 = 0.52

보통 수준의 일치: 두 관찰자는 단순히 우연에 의해 예측되는 것보다 더 자주 일치했지만, 그들의 일치도가 특별히 높은 것은 아니다.
아래 코드로 파이썬에서 카파 상관계수를 계산할 수 있다.
from sklearn.metrics import cohen_kappa_score
# 예시 데이터
observer_a = [1, 0, 1, 1, 0, 0, 1, 0, 1, 1]
observer_b = [1, 0, 1, 0, 0, 0, 1, 1, 1, 1]
# 코헨의 카파 계산
kappa = cohen_kappa_score(observer_a, observer_b)
print(kappa)
출력:
0.5833333333333333728x90
반응형
'ᐧ༚̮ᐧ Data Science | AI > 통계, 수학' 카테고리의 다른 글
| 데이터 과학자를 위한 수학 유튜브 채널 추천! (1) | 2024.11.24 |
|---|---|
| 데이터 과학자가 알아야 할 수학: 얼마나 알아야 할까? (3) | 2024.11.17 |
| [통계] p값 이해하기 (1) | 2024.11.14 |
| [딥러닝 / 수학] 코사인 유사도 cosine similarity 이해하기 (1) | 2024.06.21 |
| [통계학 with R, Python] t-검정 (t-test) (1) | 2021.09.12 |