
t-test란?
t-test는 두 집단의 평균을 비교하는 검정 방법입니다.
예를 들면, A나라의 사람들의 평균 수명과 B나라의 평균 수명을 비교하는 데에 t-test를 사용할 수 있습니다.
이때 가설은 다음과 같습니다
- 귀무가설 (null hypothesis): 두 나라의 평균 수명은 차이가 없다. (H₀: µ₁=µ₂)
- 대립가설 (althernate hypothesis): 두 나라의 평균 수명은 차이가 있다. (H1: µ₁≠µ₂)
t-test는 이렇게 두 집단을 비교할 때 사용할 수 있으며 두 집단 이상은 분산분석(ANOVA)을 사용합니다.
또, t-test는 표본이 독립성 (independent), 정규성 (Normally distributed), 등분 산성 (homoscedasticity)을 만족시킨다는 가정하에 사용할 수 있습니다.
t-test 종류

- 단일표본 (one-sample) t-test: 한 집단의 평균이 기준값(모집단의 평균)이랑 같은지 검정하는 것.
- 예제1)예제 1) 마라톤 선수들의 맥박수가 모든 운동선수들의 평균 맥박수와 다른지 비교
- 예제2) A 고등학교 학생들의 평균 IQ가 전국 고등학교 학생들의 평균 IQ와 다른지 비교
- 독립표본 (independent) t-test: 두 집단이 서로 다른 모집단에서 추출된, 독립된 두 집단의 평균의 차이를 검정하는 것
- 예제1) A 고등학교 학생들의 평균 IQ가 B 고등학교 학생들의 평균 IQ와 차이가 있는지 비교
- 예제2) A 브랜드사 닭가슴살과 B 브랜드사 닭가슴살의 단백질 함량에 차이가 있는지 비교
- 대응표본 (paired) t-test: 하나의 집단의 전과 후의 차이를 비교하는 것
- 예제1) 동영상 강의를 듣기 전과 후의 시험 성적에 차이가 있는지 비교
- 예제2) 치료를 받기 전과 후의 콜레스테롤 레벨에 차이가 있는지 비교
t-값 구하기
t 값은 t-test에서 이용되는 통계량입니다.

단일 표본 t-test 공식
x̅ = 표본 평균, μ_0 = 모집단의 평균
s = 표본표준편차, n = 표본의 수
독립 표본 t-test 공식
- 동일한 표본 크기 (n)와 분산일 경우의 공식

x̅_1 = 1번 집단의 표본 평균, x̅_2 = 2번 집단의 표본 평균,
s_p = 통합 분산 추정량
n = 표본의 수
s_x_1 = 1집단의 표본표준편차
s_x_2 = 2집단의 표본 표준편차
- 동일하거나 동일하지 않은 표본 크기에 동일한 분산

x̅_1 = 1번 집단의 표본 평균,x̅_2 = 2번 집단의 표본 평균,
s_p = 통합 분산 추정량
n_1 = 1집단의 표본의 수, n_2 = 2집단의 표본의 수
s_x_1 = 1집단의 표본 표준편차
s_x_2 = 2집단의 표본 표준편차
대응표본 t-test 공식

d = 두 집단 차이의 평균
s = 두 집단 차이의 표본 표준편차
n = 표본의 수
R에서 t-test
R에서는 t.test() 함수를 사용하여 t-test를 실행할 수 있습니다. (출처: R documentation)
t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0, paired = FALSE, var.equal = FALSE, conf.level = 0.95, …)- x - 숫자형 벡터
- y - (선택) 숫자 벡터
- alternative - 대립 가설 ("two.sided" - (기본값) 평균에 차이가 있다, "less", "greater" 평균이 더 작거나 크다)
- mu - 평균값
- paired = FALSE - (기본값) 대응표본 t-test를 할 땐 TRUE
- var.equal = FALSE - 분산이 동일할 경우 TRUE
- conf.level = 0.95 신뢰구간
R 예제
- 단일 표본 (one-sample) t-test
전국 고등학생의 평균 IQ가 108이라고 했을 때 A 고등학교 학생들의 표본과 비교해 t-통계량을 계산해보겠습니다.
avg_iq <- c(100, 110, 98, 101, 105) t.test(avg_iq, mu = 108)
t-통계량은 = -2.4405에 p-value는 0.07117로 나왔습니다.
p-value가 0.05보다 크므로 귀무가설을 채택하며 A 고등학교 학생들의 평균 IQ는 전국 고등학생의 평균 IQ와 차이가 없다고 판단할 수 있습니다.
- 독립 표본 (independent) t-test
A 고등학교 고등학생의 평균 IQ와 B 고등학교 학생들의 평균 IQ를 비교해보겠습니다.
avg_iq_A <- c(100, 110, 98, 101, 105) avg_iq_B <- c(104, 100, 107, 104, 102)
위에서 본 공식과 같이 등분산 여부에 따라 t-test에 차이가 있어 독립표본 t-test를 적용하기 전에 등분산 검정을 실시해야 합니다. 등분산 검정 방법 중 하나인 Barlett's test를 먼저 수행해보겠습니다.
bartlett.test(list(avg_iq_A, avg_iq_B))
p-value가 0.05보다 크기 때문에 두 표본의 분산에 차이가 없는 것으로 판단하겠습니다.
등분산 가정이 가능하기에 아래에 var.equal=TRUE를 넣어 t.test를 실행하겠습니다.
t.test(avg_iq_A, avg_iq_B, var.equal=TRUE)
t-통계량은 = -0.24702에 p-value는 0.8129로 나왔습니다.
p-value가 0.05보다 크므로 귀무가설을 채택하고 두 고등학교의 평균 IQ에 차이가 없다고 판단할 수 있습니다.
- 대응표본 (paired) t-test
A 고등학교 학생들의 특별과외 전(test_1)과 후(test_2)의 시험 성적을 비교해보겠습니다. 대응표본 t-test는 paired = TRUE를 넣어서 실행해야 합니다.
test_1 <- c(35, 50, 90, 78, 23) test_2 <- c(67, 72, 94, 91, 41) t.test(test_1, test_2, paired = TRUE)
t 통계량은 -3.8264이며 p-value는 0.01868입니다.
p-value가 0.05보다 작기 때문에 귀무가설을 기각할 수 있고, 특별 과외를 받기 전과 후의 성적에는 차이가 있다고 판단할 수 있습니다.
Python
R과 동일한 예제를 사용하여 파이썬에서 t-test를 실행해보도록 하겠습니다.
파이썬에서는 scipy 패키지를 사용합니다.
from scipy import stats
단일 표본 (one-sample) t-test
파이썬 scipy.stats.ttest_1samp() 함수를 이용하여 단일 표본 t-test를 수행할 수 있습니다.
전국 고등학생의 평균 IQ가 108이라고 했을 때 A 고등학교 학생들의 표본과 비교해 t-통계량을 계산해보겠습니다.
avg_iq = [100, 110, 98, 101, 105] stats.ttest_1samp(avg_iq, popmean=108)
t-통계량은 = -2.44048에 p-value는 0.07117로 나왔습니다.
p-value가 0.05보다 크므로 귀무가설을 채택하며 A 고등학교 학생들의 평균 IQ는 전국 고등학생의 평균 IQ와 차이가 없다고 판단할 수 있습니다.
독립 표본 (independent) t-test
파이썬 scipy.stats.ttest_ind() 함수를 이용하여 독립표본 t-test를 수행할 수 있습니다.
A 고등학교 고등학생의 평균 IQ와 B 고등학교 학생들의 평균 IQ를 비교해보겠습니다.
avg_iq_A = [100, 110, 98, 101, 105] avg_iq_B = [104, 100, 107, 104, 102] stats.ttest_ind(avg_iq_A, avg_iq_B, equal_var=True)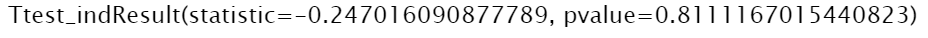
t-통계량은 = -0.24702에 p-value는 0.8129로 나왔습니다.
p-value가 0.05보다 크므로 귀무가설을 채택하고 두 고등학교의 평균 IQ에 차이가 없다고 판단할 수 있습니다.
대응표본 (paired) t-test
파이썬 scipy.stats.ttest_rel() 함수를 이용하여 대응표본 t-test를 수행할 수 있습니다.
A 고등학교 학생들의 특별과외 전(test_1)과 후(test_2)의 시험 성적을 비교해보겠습니다.
a = [35, 50, 90, 78, 23] b = [67, 72, 94, 91, 41] stats.ttest_rel(a, b)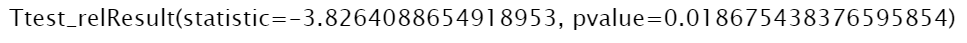
t 통계량은 -3.8264이며 p-value는 0.01868입니다.
p-value가 0.05보다 작기 때문에 귀무가설을 기각할 수 있고, 특별 과외를 받기 전과 후의 성적에는 차이가 있다고 판단할수있습니다.
'ᐧ༚̮ᐧ Data Science | AI > 통계, 수학' 카테고리의 다른 글
| [통계] p값 이해하기 (1) | 2024.11.14 |
|---|---|
| [딥러닝 / 수학] 코사인 유사도 cosine similarity 이해하기 (1) | 2024.06.21 |
| [통계] 결합확률분포 Joint Distributed Random Variables (0) | 2021.06.15 |
| [통계] 확률변수, 확률분포 (1) | 2021.06.12 |
| [통계] 척도 (Scale)의 4가지 종류: 명목 척도, 서열 척도, 구간 척도, 비율 척도 (7) | 2021.05.27 |